Data structures: Bloom filter

As we all know, there is a vast number of data structures out there. One of the data structure categories is probabilistic data structures. Probabilistic data structures usually trade certainty in their outcomes for space or time efficiency gains. In several cases, probabilistic data structures use hash functions to randomize and represent sets of data. Some of the most well known probabilistic data structures are:

• Bloom filter
• Cuckoo filter
• HyperLogLog
• MinHash

Recently, I worked with Bloom filters in order to deal with an infrastructure / cost optimization task. So, what exactly are Bloom filters?

A Bloom filter is a data structure for testing membership of an element in a set. Kind of checking the membership of a key in a hash table. The main difference is that Bloom filter uses a different storage mechanism, with the help of hash functions, in order to reduce the space needed to store data. This storage gain comes at the expense of getting a definitive answer, i.e. we might get some false positives about membership of an element in a set.

Let’s see how it all works. At the heart of a Bloom filter is a bit array of size m. Initially the bit array is filled with zeros:

Another important part of the Bloom filter is its hash functions. We choose k different hash functions. The hash functions should be carefully selected in order to produce a uniform distribution of output, otherwise the Bloom filter will suffer from a high number of false positives.

Once we have our hash functions, whenever we want to add a new member to the Bloom filter, we run all hash functions with the element as their argument and calculate the modulo of the result with the size of the bit array:

# Example:
# Size of bit array is m = 10
# Number of hash functions is k = 3

hash1("cat") % 10 = 5
hash2("cat") % 10 = 2
hash3("cat") % 10 = 8

We then set the bits of the bit array to 1 in the positions equal to the results of the modulo above (so, in the example positions 2, 5 and 8). We repeat the same process for every new element we want to add to the Bloom filter.

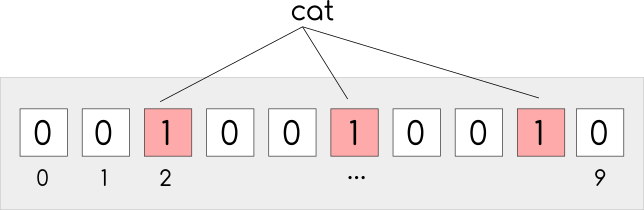
Now, when we want to test membership of an element in the set, the implementation would have to calculate the hash functions of the input and see if all the bit positions have value of 1. If so, the functions should return that the element is probably a member of the set. Why probably? Because due to the way the bit array is constructed and modified, we may have false positives as the bits might have value 1 from a combination of multiple other elements inserted in the bit array.

By tweaking the size of the bit array, the number of hash functions and the number of elements we are going to insert in the Bloom filter, we adjust the number of false positives (i.e. the probability of getting a false positive). There are numerous calculators online that, given the math behind Bloom filters, allow you calculate the size of the bit array that is needed for a specific desired probability of false positives. Here are some:

• https://hur.st/bloomfilter/
• https://toolslick.com/programming/data-structure/bloom-filter-calculator
• https://www.di-mgt.com.au/bloom-calculator.html

Benefits of Bloom filters

The most important benefit of Bloom filters is that they are very efficient at storing large sets of data. Imagine you have 1 million strings of 36 bytes each (so around 36 MBytes in size). A Bloom filter would need (you can use the calculators above to come up with the result) 3.5 MB to store everything with a probability of false positive 0.1% (so 1 false positive for every 1000 elements tested).

Also, due to the fact that they store data so efficiently, Bloom filters can be loaded in-memory e.g. once a service starts and used for fast querying based on a specific attribute (the input to our Bloom filter). An example could be filtering out traffic that does not belong to a set of mobile device identifiers in the context of mobile advertising and more specifically retargeting. Performing such a filtering without having to query a database for traffics of hundred of thousands of requests per second can be crucial to performance (and infrastructure cost).

There are several libraries that allow you build and query a Bloom filter and also store it in a file and reinstantiate it from that file (for example google’s guava set of Java libraries), which make it very easy to work with Bloom filters without having to implement them yourself.

That’s all for now!